Unit 10 Tues - Recursion
Notes + Homework
Intro to Recursion
- A recursive method is method that calls itself.
- It contains at least one base case that halts recursion and once recursive call
- Each recursive call has own local variables
- Parameter values take progress of recursive process
- A recursion can be replaced with an iterative and give the same result
- Recursion can traverse String, array, and ArrayList objects
- Can also be used with strings
// Recursion method within itself
public static void simplerRecur(int n) {
System.out.println(n);
if (n > 2)
simplerRecur(n-1);
System.out.println(n);
}
simplerRecur(4);
Binary Search w/ Equations
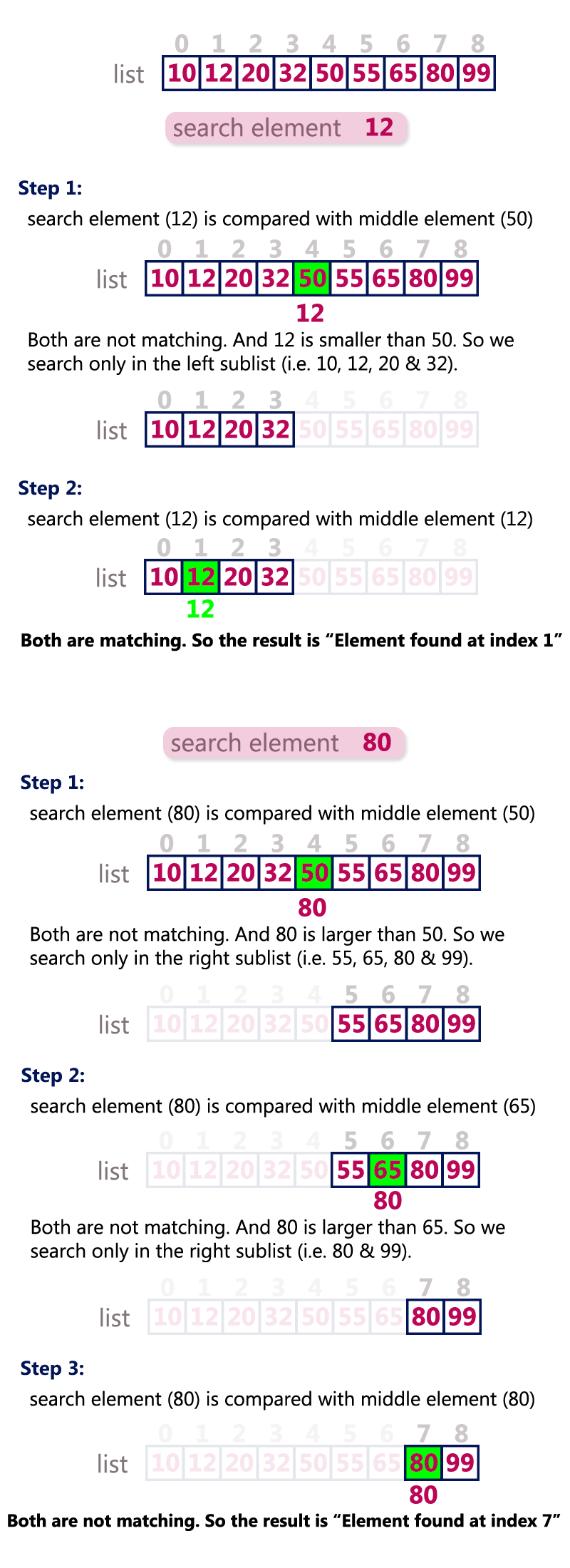
- Read the search element from the user.
- Find the middle element in the sorted list.
- Compare the search element with the middle element in the sorted list.
- If both are matched, then display "Given element is found!!!" and terminate the function.
- If both are not matched, then check whether the search element is smaller or larger than the middle element.
- If the search element is smaller than middle element, repeat steps 2, 3, 4 and 5 for the left sublist of the middle element.
- If the search element is larger than middle element, repeat steps 2, 3, 4 and 5 for the right sublist of the middle element.
- Repeat the same process until we find the search element in the list or until sublist contains only one element.
- If that element also doesn't match with the search element, then display "Element is not found in the list!!!" and terminate the function.
/**
* Recursion in binary search
*/
public class recursion{
public static int recursionBinarySearch(int[] array, int first, int last, int target){
int midpoint;
//if the first number is greater than the last, the target number is not in the list
if (first > last){
System.out.println(-1);
return -1;
} else {
midpoint = (first+last)/2;
//take the upper bound if number is greater than midpoint
if (array[midpoint] < target){
return recursionBinarySearch(array, midpoint+1, last, target);
}
// take the lower bound if the number is lesser than midpoint
if (array[midpoint] > target){
return recursionBinarySearch(array, first,midpoint-1, target);
}
System.out.println("index of target: " + midpoint);
return midpoint;
}
}
public static void main(String[] args){
// test array in main
int[] test_array = new int[]{ 0,2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,32,34,36,38,40 };
recursion.recursionBinarySearch(test_array, 0, test_array.length, 24);
}
}
recursion.main(null);
Merge Sort
- Merge Sort can be used to sort ArrayLists
- Uses a Divide and Conquer algorithm to Sort ArrayList
- Divides the array into halves, and then calls itself for the two different halves in order to sort them
- Merges the two sorted halves into one lists
- Merging Values into One Sorted Array
- copy the original elements into a temporary array
- work from left to right in each virtual array to compare element and return them to the correct order in the original array
mergeSort (myArray, low, high) {
if (low < high) {
middle = (low + high) / 2;
mergeSort(myArray, low, high);
mergeSort(myArray, middle + 1, high);
merge(myArray, low, middle, high);
}
}
Recursion Trees
- Recursion trees are a method for visualizing each recursive case (everytime the method is called) until the base case is reached.
- Recursive blocks call themselves. In order for them to finish, there must be some special case in which they don't call themselves. That is the base case, a simpler version of the block's script that doesn't call the block itself.
- There is usually a conditional with two cases: a base case for the lowest level that stops the recursion from going on forever and a recursive case that calls the block itself at lower levels until it reaches the base case.
- Note: If a block keeps recursively calling itself forever, the program is stuck in an infinite loop meaning that there isn't a base case or it is not accessible.
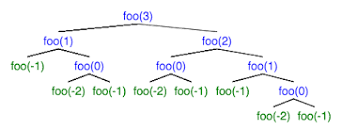
public class example{
static int foo(int n) {
if (n < 0){
return 1;
}
else{
return foo(n-2) + foo(n-1);
}
}
public static void main(String args[]){
System.out.println(foo(3));
}
}
example.main(null);
/**
* Fibonacci Series Using Recursion
*/
class fibonacci {
static int fib(int n)
{
// Handling base case
// iIf value of n=1 or n=0, it returns 1
if (n <= 1)
return n;
// Generic case
// Otherwise we do n-1 + n-2!
return fib(n - 1) + fib(n - 2);
}
public static void main(String args[])
{
// Calling method 1 to compute fibonacci and
// storing the result into a variable
int n = 3;
// Print and display the fibonacci of number
// customly passed as an argument
System.out.println("3rd Fibonacci Sequence is: " + fib(n));
}
}
fibonacci.main(null);
class factorial {
static int fact(int n) {
// Handling base case
// iIf value of n=1 or n=0, it returns 1
if (n == 0 || n == 1)
return 1;
// Generic case
// Otherwise we do n*(n-1)!
return n * fact(n - 1);
}
// Method 2
// main driver method
public static void main(String[] args) {
// Calling method 1 to compute factorial and
// storing the result into a variable
int n = 4;
// Print and display the factorial of number
// customly passed as an argument
System.out.println("Factorial of 4 is: " + fact(n));
}
}
factorial.main(null);